Finite volume method (FVM) is the universal method to be used for irregular and curvilinear grids.
About 80% of all commercial computational fluid dynamics (CFD) packages use FVM.
Equations of FVM are usually resulted from applying some conservation laws.
Indeed, most PDE of mathematical physics are derived from more general conservation laws, such as laws of mass, momentum or energy conservation.
FVM is based on using integral conservation law for each volume cell V
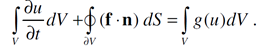
The essence of this law is the following – the speed of changing of quantity u in volume V is equal to the quantity of flow of u through the boundary of volume V plus the energy of sources of quantity u inside V.
Integral equations of this type are actually more powerful instrument then PDE, for which they are written, in the sense that they can describe, in particular, some non-continues solutions, such as shock waves, contact laceration on the boarder of two environments, and so on.
Integral equations, like the equation written above, are the primary equations in mathematical physics. These are the equations that are derived from some conservation laws.
After that, assuming smoothness of solution u and function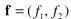 
one can obtain corresponding PDE:
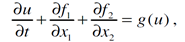
For smooth functions this differential form of equation and its integral form, written above, are equivalent - this the consequence of the Gauss-Ostrogradsky theorem (known also as a divergence theorem), but for FVM method the integral form is more convenient.
In FVM linear equations with matrices similar to those that we obtained using finite differences method (FDM), are build using approximation of integrals from integral equations for each small volume cells.
The whole system of equations that appears as a result of this approximation is, actually, the expression of a conservation law while transferring of some entity (it doesn’t matter what is transferring) between the cells of the region.
One of the main advantages of FVM (besides the fact that it is convenient for problems with irregular grid) is in the fact that it is appropriate both for Dirichlet and Neumann boundary conditions.
On the other hand, while working with regular grids (and using Dirichlet boundary condition) the method of finite differences is more suitable and provides more accurate solution.
For more details on how to use finite differences method in elliptic problems go to this page.